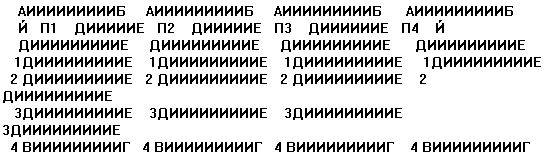Задача 1. Мультипроцессорная система (10 баллов)

4 процессора объединены в линейку (см. рис. 1). У каждого процессора есть память, состоящая из 4 занумерованных ячеек для хранения чисел. Все процессоры работают синхронно, каждый по своей программе, выполняя за 1 такт 1 команду из следующей системы команд:

• А i, j, k - сложить содержимое i-той ячейки с содержимым j-той ячейки и результат поместить в к-тую ячейку;
• M i, j, k - умножить содержимое i-той ячейки на содержимое j-той ячейки и результат поместить в к-тую ячейку;
• R i, j - переслать содержимое i-той ячейки в j-тую ячейку процессора, расположенного справа;
• L i, j - переслать содержимое i-той ячейки в j-тую ячейку процессора, расположенного слева;
• N - один такт ничего не делать.

Написать программы для каждого процессора, чтобы результатом их работы являлось значение многочлена:

Задача 2. (7 баллов).

На квадратном листе клетчатой бумаги размером NxN в каждой клетке записано число от 0 до 7. Если числа в двух клетках с общей стороной отличаются ровно на 1, то в обе клетки записывается большее из них. На каждом шаге производится сравнение ровно двух клеток, начиная с верхней левой клетки.

а) Разработать алгоритм, который осуществляет описанную процедуру до тех пор, пока это возможно. (4 балла).

б) Зависит ли результат от порядка перебора клеток? (1 балл)

в) Конечен ли этот процесс? (2 балла)

Задача 3. Торт (6 баллов)

На квадратном торте стоит N свечей. Можно ли одним прямолинейным разрезом разделить его на две равные по площади части, одна из которых не содержала бы ни одной свечи? Свечи считать точками, каждая из которых задана парой целочисленных координат относительно центра торта; разрез не может проходить через свечу.

Задача 4 (8 баллов)

Сложение с помощью логических операций. Составить программу, которая выполняет сложение двух пятиразрядных двоичных чисел, пользуясь операциями "И", "ИЛИ", "НЕ" и "СДВИГ ВЛЕВО"(на один разряд), которые выполняются так:

1) C=BA переменной С присваивается значение числа А, в котором нули заменяются на 1, а единицы на 0(Операция "НЕ");

2) C=AvB поразрядная операция, в которой каждый разряд перемен ной С получает значение, вычисленное по значениям соответствующих разрядов А и В согласно таблице 1(Операция"ИЛИ");

3) С=А^В поразрядная операция, в которой каждый разряд переменной С получает значение, вычисленное по значениям соответствующих разрядов А и В согласно таблице 2(Операция "И");

4) С=<BA поразрядный сдвиг влево, т. е., i-тый разряд Сполучает значение i+1-го разряда числа А, 5-тый(младший) разряд С становится равным 0. Каждое из исходных чисел меньше 10000.

Задача 5 (6 баллов)

F(x) - процедура, вычисляющая значение непрерывной функции, которая определена на всей действительной оси, убывает при всех х, меньших некоторого числа х0, и возрастает при всех х, больших, чем х0.

Составить алгоритм, который определяет х0 с точностью Е.

Задача 6 (10 баллов)

ЭВМ 1 и ЭВМ 2 имеют общий однобитовый регистр R, в который они могут записывать информацию и из которого они могут читать. Их система команд, кроме традиционных, дополнена тремя дополнительными командами: чит(К) - переменной К присваивается значение регистра R;зап(К) - значение К (0 или 1) записывается в R;пауза - задерживает процесс вычислений на время, в 10раз большее, чем время выполнения любой другой команды (все остальные команды выполняются за одинаковое время).

Программа П2 запускается на ЭВМ 2 раньше, чем программа П1на ЭВМ 1. Во время работы П1 с клавиатуры ЭВМ 1 вводится последовательность двоичных цифр 1, 0, 1, 1, 1, 0, 0, 1. Что напечатает ЭВМ 2 ?

Ответ обосновать.

Задача 7 (5 баллов)

Дан выпуклый N-угольник координатами своих вершин. Найти наибольшую по длине диагональ и напечатать вершины, которые она соединяет.

Задача 8 (3 балла)

Даны 3 вершины прямоугольника своими координатами. Найти координаты четвертой его вершины.

Задача 9 "Болезнь ЭВМ" (2 балла)

Доказать, что в 16-разрядной ЭВМ с объемом ОЗУ 128 Кбайт в любой момент времени T существуют две ячейки, содержащие одинаковые числа.